
Classification And Regression Trees (CART) 는 Classification와 regression 문제 모두 처리 가능한 Binary Decision Tree를 훈련시키는 알고리즘.
1. 역사적 배경
- 1984년 Leo Breiman, Jerome H. Friedman, Richard A. Olshen, Charles J. Stone 저서 Classification and Regression Trees 에서 등장:
- AID(1963), THAID(1972) 등의 트리 기반 분할 연구를 계승.
- “binary split”과 “purity” 개념을 명확히 정립: gini 계수 사용하여 impurity를 측정.
다른 Decision Tree Algorithms(ID3, C4.5 등)과 달리 regression 을 다루도록 확장된 차이점을 가지며, Random Forest, XGBoost, LightGBM 등 앙상블 알고리즘의 기본요소로 가장 널리 사용됨.
Iterative Dichotomiser3 (ID3) 와 C4.5는
다중노드를 사용하며
classification만을 지원한다는 차이점도 있음
2. 알고리즘 핵심 구조
- 입력 데이터: ($m$)개의 학습 샘플.
- 분할 기준: 단일 feature $k$와 해당 feature를 2개의 자식노드로 나눌 threshold $t_k$.
Objective function (or Cost function)은 다음과 같음:
$$J(k,t_k)=\frac{m_\text{left}}{m}G_\text{left}+\frac{m_\text{right}}{m}G_\text{right}$$
where
- $G$: classification에선 impurity measure (Gini, Entropy 등), regression에선 MSE.
- $m_\text{left}, m_\text{right}$: 좌우 자식 노드로 나누어진 샘플 수.
CART는 위의 $J(k,t_k)$ 를 최소화하도록 최적 분할 후 좌우 노드의 서브셋에 대해 재귀적으로 분할을 수행.
훈련의 종료 조건은 다음과 같음:
max_depth(최대깊이) 도달 시.- 더 이상 impurity 감소가 불가능한 경우
min_samples_split,min_samples_leaf등을 만족시킬 수 없는 경우 (최소 샘플 수 제약).
CART는 greedy algorithm임:
- 각 단계에서 지역 최적(local optimum) 선택.
- 이 경우 계산 복잡도가 $O(m \times n \times \log n)$임: Polynomial Time.
- 단, 이 경우 전체 트리의 전역 최적(global optimum)은 보장하지 않음.
- CART는 합리적으로 좋은(reasonably good)” 근사 해 제공
가능한 모든 Tree 조합을 검색한다면 최적의 Tree를 찾을 수 있음:
- 최적 트리 탐색: NP-Complete 문제로 계산 복잡도 $O(\exp(m))$.
NP-Complete는
다항시간에 solution 검증이 가능한 NP 문제이나,
실제로 solution을 구하기가 NP 중 가장 어려운 문제임.
모든 NP 문제들이 다항시간 내에 NP-Complete로 reduction(환원)가능함.
참고: Gini Coefficient
Gini impurity measure에서 "Gini"는 줄임말이 아닌 이탈리아의 통계학자이자 사회학자인 Corrado Gini의 이름에서 유래한 용어. Gini는 불평등을 측정하는 Gini 계수로 유명한데, 이 개념이 결정 트리에서 불순도를 측정하는 데 사용됨.
$$ \text{Gini} = 1 - \sum_{i=1}^{n} (p_i^2) $$
- $n$ : number of classes
- $p_i$ :현재 노드에서 인스턴스가 클래스 $i$ 에 속할 확률.
- CART는 binary trees가 사용되기 때문에 클래스는 보통 2개임.
0이면 불순도 0의 순수한 노드임.
참고: Gini vs. Entropy
gini와 entropy 중 무엇을 사용하느냐는 Decision Tree에서 큰 차이는 없으나, 기본값인 gini가 좀 더 계산속도가 빠르고 `entropy`는 좀 더 balanced tree를 만든다고 알려짐.
노드에서 54개의 instance가 있고, 49개의 클래스A, 5개의 클래스B인 경우, gini는 0.168이고 entropy는 0.445임.
gini : $1- \left\{ \left( \frac{49}{54} \right) ^2 + \left(\frac{5}{54}\right)^2\right\} \approx 0.168$
entropy: $–(49/54) \log_2 (49/54) – (5/54) \log_2 (5/54) \approx 0.445$
gini가 0이면 순수한 노드인 것처럼, Entropy도 0이면 순수한 노드이고 클수록 불순도가 큼.
https://dsaint31.tistory.com/291
[Math] Entropy 란 (평균정보량, 정보량의 기댓값)
Entropy란?Random variable에서 기대되는 정보량 (or 정보량의 기댓값, 평균 정보량).해당 random variable을 encoding하는데 필요한 평균정보량(단위 bit)의 lower bound.Claude Shannon 이 1948년 증명한 Noiseless Coding The
dsaint31.tistory.com
3. 알고리즘 특징
- 구조: binary tree.
- 분류용 순도 척도: Gini, Entropy.
- 회귀용 손실 척도: MSE, MAE 등.
- 학습 방식: Recursive Partitioning(재귀적 분할).
- 가지치기(Pruning) : 과적합 방지를 위한 후처리 가능.
Decision Tree는 Non-parameteric model이기 때문에, 훈련 전에 parameters의 수가 미리 결정되어있지 않음.
이는 비선형 관계를 잘 학습할 수 있고, 결측치에 강하고 input data의 scale difference에 영향이 없어서 feature scaling이 필요없다는 장점을 가지지만,
훈련 데이터에 의해 parameters의 수가 결정되는 구조라 DoF가 매우 높아서 over-fitting되기 쉬움.
(Decision Tree는 트리의 구조와 parameters의 수가 훈련데이터에 의해 결정됨)
Decistion Tree는 매우 variance가 높기 때문에 training dataset의 미세한 차이가 훈련된 모델에서 큰 차이로 이어지기 때문에 stability가 매우 낮은 편이기 때문에 여러 Decistion Trees를 훈련시켜서 averaging하는 ensemble 기법이 보다 많이 애용된다.
Random Forest, Gradient Boosting Trees 등 ensemble 기법 사용하면 variance를 줄여주어 generalization performance가 향상됨.
4. Regularization for Decision Tree
Decision Tree의 단점인 overfitting을 막기 위한 regularization을 위해 다음의 parameters가 보통 제공됨:
- max_depth : root가 depth=0 로서 작은 수의 깊이일수록 강한 regularization임.
- max_leaf_nodes : 최대 leaf nodes의 수. 작을수록 강한 regularization.
- max_features : 각 node에서 splitting을 위해 확인해봐야 하는 features의 수. 작을수록 강한 regularization.
- min_samples_split : node에서 splitting을 위해 최소한 있어야하는 샘플의 수. 클수록 강한 regularization
- min_samples_leaf : leaf node 가 가져야하는 최소한의 샘플 수. 클수록 강한 regularization.
- min_weight_fraction_leaf : min_samples_leaf와 같은 효과를 주는 하이퍼파라미터로 leaf node에 포함되어야 하는 최소 샘플비율임(전체 샘플수에 대한 비율). 클수록 강한 regularization.
다음은 CART가 restriction이 없는 경우와 min_samples_leaf 를 통한 regularization을 한 경우 결과를 보여줌.


Decision Tree의 overfitting을 막기 위한 다른 방법으로는 Post-pruning임.
Post-pruning은 제약없이 Tree를 완전히 training(=growing)하고 나서, 불필요한 leaf node를 제거하는 것
- 해당 leaf node가 제공하는 purity 개선이 통계적으로 유의미한지를 chi square 검정 등을 통해 테스트하고 유의미하지 않은 경우 불필요한 노드로 간주하여 삭제하는 것임.
- 보통, Chi square 통계량을 계산하고 이에 대한 p-value를 구하고 alpha (가설검증의 유의수준. 보통 0.05) 를 초과하는 경우 해당 노드를 삭제함.
Scikit-learning 에서는 Cost-Complexity Pruning 을 통해 pruning을 제공함(완전한 의미의 post-pruning은 아니지만 효과는 동일)
다음은 충북대학교 정보통계학과 나종화 교수님의 예제임.

이에 대한 p-value를 계산하는 방법은 다음과 같음:
import numpy as np
import scipy.stats as stats
import pandas as pd
import matplotlib.pyplot as plt
from IPython.display import Math, HTML
def report(chi2, p_value, dof, expected, idx=None, col=None):
display(Math(r'\chi^2 :'+ str(chi2)))
print('p-value :', p_value)
print('dof :', dof)
display(pd.DataFrame(data=expected, index=idx, columns=col))
node = ['left','right']
cls = ['A','B']
data = np.array([
[6,2],
[0,4],
])
df = pd.DataFrame(
data = data,
index = node,
columns = cls,
)
display(df)
# To reproduce the result on Howell's book,
# correction= False is used.
report(*stats.chi2_contingency(df,correction=False),node, cls)결과는 다음과 같음:
5. Cost-Complexity Pruning
모델 복잡도 (=leaf 수) 와 적합도 (오차) 사이의 균형을 조절함.
Cost Function이 다음과 같음:
$$R_\alpha (T) = R(T) + \alpha |T|$$
where
- $R(T)$: Tree $T$의 전체 Cost (Gini or MSE 등등)
- $|T|$: Tree $T$의 lean nodes의 개수
- $\alpha$ :
ccp_alpha(Cost-Complexity Pruning Alpha). pruning 강도조절 hyperparameter- $\alpha >0$ 으로 증가시 : leaf nodes가 많은 복잡한 Tree에 보다 큰 패널티 부여.
- $\alpha =0$ : 가장 깊은 (over-fitted) Tree 가 훈련됨(가장 많은 lean nodes를 가짐)
scikit-learn에선 post-pruning기법과 같은 효과를 내도록
사전시뮬레이션으로 주요 ccp_alpha들을 구하고
CV를 통해 최적의 ccp_alpha를 구해서 최적의 Tree를 구함.
5. scikit-learn 구현
- 클래스:
DecisionTreeClassifier,DecisionTreeRegressor. - 내부 구현: CART 알고리즘의 optimized version 사용.
- 지원 기능:
- continuous feature 자동 분할.
criterion:gini,entropy,mse,mae등 선택 가능.- 조절 파라미터:
max_depth,min_samples_split,min_samples_leaf,max_leaf_nodes등.
- 미지원 사항:
- categorical feature 직접 분할 못 함(one-hot encoding 으로 전처리 필요).
- 시간 복잡도: ($O(n_{\text{samples}} \cdot n_{\text{features}} \cdot \log n_{\text{samples}})$).
- Cost-Complexity Pruning의 최적의 alpha를 구하기 위해 완전한 트리(
fit된 트리모델객체t) 에서 루트 만 남을 때까지의 모든 중간 단계 의 임계 alpha값들의 리스트를t.cost_complexit_pruning_path(X,y)메서드를 통해 반환.path = t.cost_complexity_pruning_path(X_train, y_train):t는 제약없이 overfitted tree임.path.ccp_alphas가 주요 임계 alpha값들의 리스트이고,path.impurities는 각 alpha에 대응하는 불균일도임.
6. 요약 및 주의사항
- CART: 1984년 Breiman 등에 의해 제안된 이진 결정트리 알고리즘.
- 목적: 순도를 최대화하는 이진 분할을 재귀적으로 수행.
- 특징: 탐욕적(greedy) 분할 + 순도 기반 비용 최소화.
- 한계: 전역 최적 보장 불가, NP-Complete 복잡도.
- Cost-Complexity Pruning: 비용-복잡도 가지치기(
ccp_alpha) 도입으로 트리 단순화 및 과적합 억제. - 구현: scikit-learn의 최적화된 CART 버전이 대표적 실무 구현체.
- 활용: 분류, 회귀, 앙상블(랜덤포레스트 등) 기반 모델의 핵심 구성요소.
참고로, CART는 feature가 하나의 축이라 보고 해당 축에 직교하는 dicision boundary가 생성되기 때문에 축에 따라 성능이 매우 영향을 받게 되므로 PCA를 통해 적절한 축(서로에게 직교하는)으로 feature engineeering을 해주는 것이 일반적임.
(단 PCA를 하게될 경우 해석이 용이성이 축의 변화로 인해 조금 어려워짐)

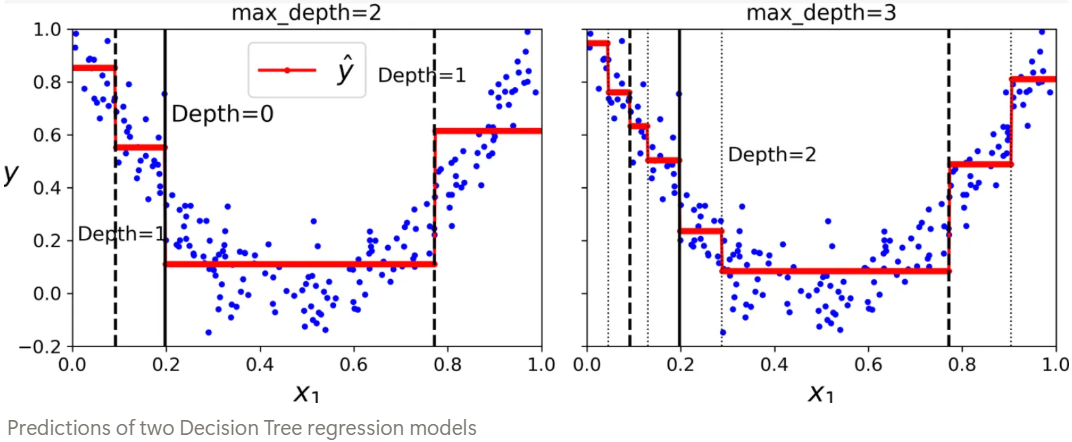
CART를 통한 regression (Decisiont Tree기반 regression의 공통적 특성)은 extrapolaration이 안된다는 단점이 있음에 유의할 것: piecewise constant model 로 training dataset이 다루지 않는 범위밖을 예측하는데에선 사용해선 안됨.

7. 예제
Iris 데이터셋을 이용한 classification 예제임:
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
import numpy as np
# -----------------------
# 0.Iris 데이터셋 로드 (4개의 feature, 3개의 클래스)
iris = load_iris()
X = iris.data
y = iris.target
# stratify=y : 각 클래스 비율이 train/test 모두 동일하게 유지됨
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y,random_state=42)
# -----------------------
# 1. 완전한 트리로 pruning path 계산
# 제한 없는 트리(max_depth 미설정)로 먼저 학습하여,
# 이후 pruning(가지치기) 경로(cost_complexity_pruning_path)를 계산하기 위해서임
clf = DecisionTreeClassifier(random_state=42)
clf.fit(X_train, y_train)
print(f"full tree의 깊이: {clf.get_depth()}")
print("--------------")
# -----------------------
# 2. post-pruning 시뮬레이션
# cost_complexity_pruning_path() :
# - α(ccp_alpha) 값에 따라 트리를 가지치기할 때의 불순도(impurity) 변화를 계산
# - ccp_alpha가 커질수록 트리가 단순해짐
path = clf.cost_complexity_pruning_path(X_train, y_train)
ccp_alphas = path.ccp_alphas
impurities = path.impurities
print(f"ccp_alphas (임계 alpha 값들):")
print(ccp_alphas)
print(f"impurities (각 alpha에서의 effective impurity):")
print(impurities)
print("--------------")
# 3. 각 alpha로 교차 검증
# 목적: validation score를 통해 최적의 α 선택
# cross_val_score()로 K-Fold 교차검증 (cv=5)
from sklearn.model_selection import cross_val_score
cv_scores = []
for ccp_alpha in ccp_alphas:
clf = DecisionTreeClassifier(random_state=42, ccp_alpha=ccp_alpha)
scores = cross_val_score(clf, X_train, y_train, cv=5)
cv_scores.append(scores.mean())
print(f"{cv_scores = }")
# 4. 최적 alpha 선택
# 가장 높은 평균 교차검증 점수를 주는 α 선택
optimal_alpha = ccp_alphas[np.argmax(cv_scores)]
print(f"최적 ccp_alpha: {optimal_alpha:.4f}")
# 5. Cost-Complexity Pruning 적용
# 최적 alpha로 Cost-Complexity Pruning 적용 후 재학습
clf_pruned = DecisionTreeClassifier(random_state=42, ccp_alpha=optimal_alpha)
clf_pruned.fit(X_train, y_train)
print(f"\nWith pruning - Nodes: {clf_pruned.tree_.node_count}")
print(f"Test accuracy: {clf_pruned.score(X_test, y_test):.3f}")
결과는 다음과 같음:
full tree의 깊이: 6
--------------
ccp_alphas (임계 alpha 값들):
[0. 0.00669643 0.00867347 0.01339286 0.02266484 0.26355965
0.33625638]
impurities (각 alpha에서의 effective impurity):
[0. 0.01339286 0.0307398 0.04413265 0.06679749 0.33035714
0.66661352]
--------------
cv_scores = [np.float64(0.9292490118577075), np.float64(0.9292490118577075), np.float64(0.9292490118577075), np.float64(0.9375494071146244), np.float64(0.9375494071146244), np.float64(0.8648221343873518), np.float64(0.46640316205533594)]
최적 ccp_alpha: 0.0134
With pruning - Nodes: 7
Test accuracy: 0.895
같이보면 좋은 자료들
https://dsaint31.tistory.com/854
[ML] Feature Importances for Decision Tree
이 문서는 Feature Importance를 Decision Tree에서 Gini Impurity Measure를 이용하여 계산하는 예제를 보여줌.Tree 예시 (depth = 3) [Root] (X1) [5:5] / \ Node1 Node2 (X2) (X3) [4:1] [1:4] / \ / \Leaf1 Leaf2 Leaf3 Leaf4[3:0] [1:1] [0:2] [
dsaint31.tistory.com
'ML' 카테고리의 다른 글
| Detection Task에서 collate_fn의 입·출력 구조와 default_collate의 한계 (0) | 2025.12.15 |
|---|---|
| [PyTorch] tensor의 vectorized operation (0) | 2025.12.04 |
| [ML] History of ML (작성중) (1) | 2024.07.08 |
| [ML] Classification 과 관련 metrics 에 대한 소개. (0) | 2024.06.01 |
| [DL] MultiLabelSoftMarginLoss: Multi-label classification (0) | 2024.05.30 |




