참고로, 이 글의 원문은 https://cmparlettpelleriti.github.io/BTC.html 임: 2024.11.14 현재 링크가 깨짐.
1. Block Truncation Coding(BTC)란
허프만 코딩 과 달리,
- BTC는 인코딩 과정에서 약간의 정보를 손실함: irreversible.
- 그러나 BTC를 이미지에 적용할 때, 발생하는 정보 손실은 종종 눈에 띄지 않거나, 적어도 이미지의 해석에 방해가 되지 않는 경우가 일반적임.
- 원본 이미지가 시베리안 허스키라면,
- BTC를 압축 후 다시 재구성된 이미지가 포메리안이 아닌 시베리안 허스키임을 인식할 수 있음.
BTC는 다음과 같은 아이디어에 기반합니다:
- 두 (확률)분포가 동일한 parameters(매개변수들)을 가지고 있다면,
- 그들은 매우 유사할 가능성이 높거나 충분히 유사하다고 애기할 수 있음.
BTC는 실제로 mean과 std를 일치하는 Block으로 압축을 수행함.
BTC는 mean과 std, 그리고 binary block으로 구성됨.
4×4 픽셀 이미지가 픽셀당 8 비트(0-255)를 가지고 있다면,
- 그 이미지를 전송(또는 저장)하기 위해
- 128비트가 필요함.
하지만 약간의 이미지 품질을 희생할 의사가 있다면 요구되는 bit의 크기를 줄일 수 있음.
아래 그림에서, 왼쪽은 레나의 원본 사진이고 가운데는 BTC로 압축된 정보 중 binary image에 해당하고, 오른쪽은 이를 복원한 영상임.

- 가운데 이미지는 원본 이미지와 같은 형태를 가진 binary matrix로 그 element(요소) 타입은 1비트(0 또는 1)임.
2. Encoding
2-1. 4×4 block 들로 image 분할
BTC를 사용하기 위해,
- 먼저 이미지를 4×4 블록으로 분할.
- 그런 다음, 16픽셀로 구성된 각각의 블록을 개별적으로 인코딩.
- 전체 512×512 이미지의 경우, 각각의 block은 매우 작은 크기를 가짐.
2-2. Block당 두 개의 대표값 계산
먼저, 블록에 대한 두 개의 대표값을 계산합니다.
일반적으로 사용되는 대표값은 픽셀값의 mean(평균)과 std(표준편차)임.
$$\bar{I} = \frac{1}{16}\sum\limits_{i = 1}^{16} I(i) \\\\ \sigma = \sqrt{\frac{1}{16}\sum\limits_{i = 1}^{16}(I(i) - \bar{I})^2}
$$
그런 다음 mean과 std를 얼마나 정확하게 표현(전송)할지 결정함.
보통 각각 8 bit 면 충분하지만, 6bit나 4bit만 사용할 수도 있음.
1개의 block에 대해 8bit로 representative value를 표현하기로 한 경우, 8 + 8 = 16 bit가 필요함.
2-3. 블록별 binary matrix 계산.
다음으로, binary 4×4 matrix (또는 binary block)를 계산함.
이 matrix에서 각 pixel은
- 대응되는 원래 픽셀이 평균보다 크거나 같으면
1을, - 평균보다 작으면
0이 할당됨.
$$
b(i)=\left\{\begin{array}
{ll}1; & \text{if I(i)} \geq \bar{I} \\ 0; & \text{otherwise.}
\end{array}\right.$$
이 이진 행렬을 저장(or 표현 or 전송)하기 위해 16bit(이미지의 각 픽셀당 1비트)가 필요함.
- 따라서 하나의 block을 저장하는 데
32bit [32 = 8(mean)+8(std)+16(binary matrix)]가 필요함. - 원본 이미지에서 하나의 4×4 픽셀 블럭을 저장하는 데 필요한 128bit [8(channel) x 4(width) x 4(height)]와 이 32bit를 비교하면, 매우 작은 값에 해당함.
2-4. Example
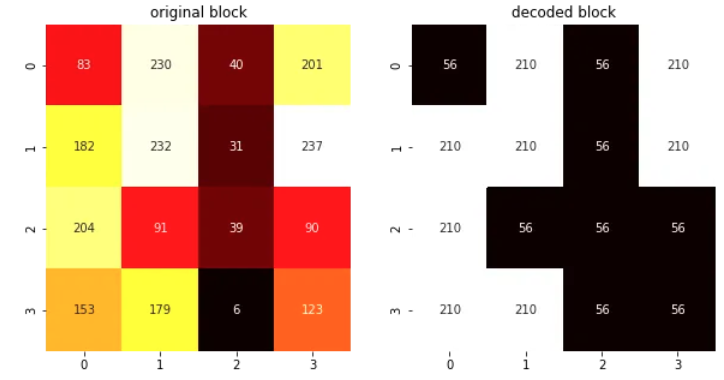
예를 들어, 하나의 gray-scale block을 BTC로 encoding한다면
- mean(~133),
- std(~77),
- binary matrix: 각 픽셀이 평균보다 높은지 낮은지를 알려줌
이 만들어짐.

3. Decoding
인코딩된 이미지의 각 4×4 블록에 대해 다시 이미지로 복원하기 위해서는 압축을 해제해야 함: 디코딩
이를 위해 먼저 저장한 이진 행렬에서 1과 0의 개수를 count(계수) 수행.
- 이는 원본 픽셀 값의 분포에 대한 많은 정보를 제공.
- 예를 들어,
- 두 데이터 세트는 동일한 평균과 표준 편차를 가진다고 가정해보자.
- 이 두 데이터 세트에서 평균 이상과 이하의 포인트 수가 다르다면, 이를 통해 이 데이터 세트를 쉽게 구분할 수 잇음.
- 데이터셋 a는 평균 이상의 포인트가 5개이고, 데이터셋 b는 2개 뿐이라고 가정하면
- 이를 통해 a와 b의 데이터 포인트가 얼마나 극단적인지에 대한 정보를 알 수 있음.
- b는 평균 이상의 포인트가 2개 뿐이지만 a와 (근사적으로) 동일한 표준 편차를 가지므로,
- b에서의 평균 이상의 두 포인트는 평균보다 매우 큰 값을 가져야 함.
이를 이용하여 decoding 하기 위해 다음과 같이 정의:
- $q$는 binary matrix에서 1의 개수이고,
- $p$는 0의 개수입니다.
그런 다음 다음과 같은 새로운 이미지 블록 $J$를 계산.
$$J(i)=\left\{
\begin{matrix}\bar{I} + \frac{\sigma}{\sqrt{\frac{q}{p}}}&; \text{ if b(i) = 1} \\
\bar{I} - \sigma \times \sqrt{\frac{q}{p}}&; \text{ if b(i) = 0}
\end{matrix}
\right.$$
$\bar{I} + \frac{\sigma}{\sqrt{\frac{q}{p}}}$와 $\bar{I} - \sigma \times \sqrt{\frac{q}{p}}$를 사용하여 새로운 블록 $J$의 평균과 표준편차는 original image의 대응되는 블록과 동일하게 됨.
$J$와 original block은 완전히 동일한 pixel을 가지지 않으나 적어도 다음 3가지 중요한 특성이 같음:
- mean,
- std (표준편차), 그리고
- 평균값보다 높은 픽셀과 낮은 픽셀의 위치.
앞서의 예에 대한 복원된 block은 다음과 같음.
4. Code for Python
사용된 Lenan이미지
5. 결론
BTC는 mean과 std를 저장하는데 사용할 bit 수에 따라 차이는 있으나, 원본을 효과적으로 compression시킴.
일반적으로 이미지에 한정한다면, 크게 인식에 지장을 주는 정도의 차이를 보이지 않으면서 매우 효과적으로 압축이 가능함.
'Python' 카테고리의 다른 글
| [Py] Higher-order Function (고차함수) (1) | 2024.11.20 |
|---|---|
| [Py] 숫자 야구 게임: structured programming, type annotation, and OOP (0) | 2024.11.20 |
| [Py] Queue 와 Stack 구현하기: 상속과 오버라이딩 이용. (1) | 2024.11.13 |
| [Py] 사칙연산 구현 예제 (0) | 2024.11.13 |
| [ML] Classic Regressor (Summary) - regression (0) | 2024.10.02 |
