728x90
반응형
vector를 이용하여 직선 간의 사이각을 구할 때에는 inner prodcut를 이용한 cos과 acos을 활용하는 경우가 많다.
하지만, unit vector를 구하고 이들간의 특정 방향 (cw or ccw)등으로 각도를 구해야하는 경우 등에서는 atan2가 보다 편하다. (대부분 사이각이 요구되지만, 특정 방향으로의 각도를 구하고 이들간의 관계가 +,-가 정해져있을 때는 atan2가 낫다.)
다음의 사용시 기억할 주요 내용임.
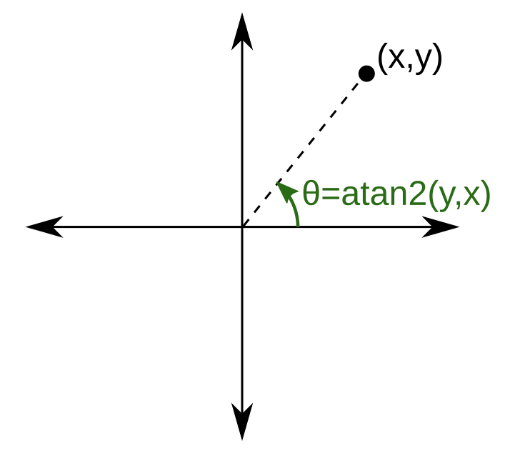
math.atan2(y, x)에는 두 개의 parameter가 있어서 direction을 나타내는 vector의 x,y component값을 넣어주면 된다.- 주의할 것은
y가 먼저 위치하고 있다는 점이다. - Python에서
math.atan2는arctan에 해당하므로 각도를 반환하며 이 단위는 radian이다. - 해당 각도는 좌표 평면에서 x축의 양의 방향으로 기준으로 ccw 를 +, cw를 -로 하며 \([-\pi, +\pi]\) 범위를 가진다.
다음 예제는 우리에게 익숙한 30도, 45도, 60도, 90도, 120도, 135도, 150도, 180도, 210도, 225도, 240도, 270도, 300도, 315도, 340도, 360도 에 대한 vector들을 입력하여 math.atan2를 통해 실제 각도가 제대로 나오는지를 확인한 예제이다.
ds_deg라는 wrapper function을 만들어서 radian을 degree로 바꿔주고, 범위를 \([0,360]\) 으로 변경해주었다.
import math
def ds_deg(y,x):
r = math.atan2(y,x)
r = math.degrees(r)
if r<0:
r = 360+r
return round(r,4) # float의 한계로 인한 오차를 없애기 위해 반올림.
angles = [0, 30, 45, 60, 90, 120, 135, 150, 180, 210, 225, 240, 270, 300, 315, 340, 360]
radians = map(lambda x: x*math.pi/180., angles)
vectors = [ (math.sin(r),math.cos(r)) for r in radians] # (y,x) tuple을 element로 가지는 list
#print(list(map(lambda x: (round(x[0],4),round(x[1],4)),vectors)))
for a, v in zip(angles, vectors):
r = ds_deg(*v)
print(f'{a} = {r} degrees') # a는 원래 나와야하는 degree, r은 atan2로 얻은 degree결과는 다음과 같음.
0 = 0.0 degrees
30 = 30.0 degrees
45 = 45.0 degrees
60 = 60.0 degrees
90 = 90.0 degrees
120 = 120.0 degrees
135 = 135.0 degrees
150 = 150.0 degrees
180 = 180.0 degrees
210 = 210.0 degrees
225 = 225.0 degrees
240 = 240.0 degrees
270 = 270.0 degrees
300 = 300.0 degrees
315 = 315.0 degrees
340 = 340.0 degrees
360 = 360.0 degrees
https://gist.github.com/dsaint31x/39ed6932d46e4a862fe9ac733bff7af8
math_atan2.ipynb
math_atan2.ipynb. GitHub Gist: instantly share code, notes, and snippets.
gist.github.com
728x90
'Python' 카테고리의 다른 글
| [Python] Dictionary's methods (0) | 2023.07.11 |
|---|---|
| [Python] 특정 점에서 직선에 수선의 발 구하기. (0) | 2023.07.11 |
| [Python] lambda expression and map, filter, reduce. (0) | 2023.07.07 |
| [Python] os 모듈의 함수들 : file과 directory 관련 (1) | 2023.07.04 |
| [Python] binary file: write and read (0) | 2023.07.04 |



